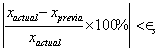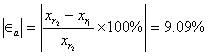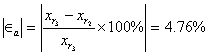El método de bisección se basa en el siguiente teorema de Cálculo:
Teorema del Valor Intermedio
Sea    contínua en un intervalo   y supongamos que  . Entonces para cada   tal que  , existe  un  tal que  . La misma conclusión se obtiene para el caso que  .
Básicamente el Teorema del Valor Intermedio nos dice que toda función contínua en un intervalo cerrado, una vez que alcanzó ciertos valores en los extremos del intervalo, entonces debe alcanzar todos los valores intermedios.
En particular, si    y   tienen signos opuestos, entonces un valor intermedio es precisamente ,  y  por lo tanto, el Teorema del Valor Intermedio nos asegura que debe existir   tal que , es decir, debe haber por lo menos una raíz de   en el intervalo .
El método de bisección sigue los siguientes pasos:
Sea   contínua,
i) Encontrar valores iniciales  ,    tales que    y    tienen signos opuestos, es decir,

ii) La primera aproximación a la raíz se toma igual al punto medio entre    y  :

iii) Evaluar  . Forzosamente debemos caer en uno de los siguientes casos:

•  

En este caso,  tenemos que    y    tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo  .

•  

En este caso,  tenemos que    y    tienen el mismo signo, y de aquí que    y   tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo  .

•  

En este caso se tiene que   y por lo tanto ya localizamos la raíz.
El proceso se vuelve a repetir con el nuevo intervalo, hasta que:

es decir,

Ejemplo 1
Aproximar la raíz de    hasta que  .
Solución
  Sabemos por lo visto en el ejemplo 1 de la sección anterior, que la única raíz de    se localiza en el intervalo  .  Así que este intervalo es nuestro punto de partida; sin embargo, para poder aplicar el método de bisección debemos checar que    y    tengan signos opuestos.
En efecto, tenemos que

mientras que

Cabe mencionar que la función    sí  es contínua en el intervalo  . Así  pues, tenemos todos los requisitos satisfechos para poder aplicar el método de bisección. Comenzamos:
i)   Calculamos el punto medio (que es de hecho nuestra primera aproximación a la raíz):

ii)   Evaluamos 
iii)   Para identificar mejor en que nuevo intervalo se encuentra la raíz, hacemos la siguiente tabla:

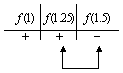
Por lo tanto, vemos que la raíz se encuentra en el intervalo  . 
En este punto, vemos que todavía no podemos calcular ningún error aproximado, puesto que solamente tenemos la primera aproximación. Así, repetimos el proceso con el nuevo intervalo  .
Calculamos el punto medio (que es nuestra segunda aproximación a la raíz):

Aquí podemos calcular el primer error aproximado, puesto que contamos ya con la aproximación actual y la aproximación previa:

Puesto que no se ha logrado el objetivo, continuamos con el proceso.
Evaluamos  , y hacemos la tabla:

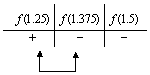
Así, vemos que la raíz se encuentra en el intervalo  .
Calculamos el punto medio,

Y calculamos el nuevo error aproximado:

El proceso debe seguirse hasta cumplir el objetivo.
Resumimos los resultados que se obtienen en la siguiente tabla:

Aprox. a la raíz	Error aprox.
1.25
1.375	9.09%
1.3125	4.76%
1.28125	2.43%
1.296875	1.20%
1.3046875	0.59%

Así, obtenemos como aproximación a la raíz

Ejemplo 2
Aproximar la raíz de   hasta que  .
Solución
 Como vimos en el ejemplo 2  de la sección anterior, la única raíz de   se localiza en el intervalo  . Para poder aplicar el método de bisección, es importante checar que sí se cumplen las hipótesis requeridas.
Sabemos que   es contínua en el intervalo , y checamos que   y   tengan signos opuestos.
En efecto,

Mientras que,

Por lo tanto, sí podemos aplicar el método de bisección.
Calculamos el punto medio del intervalo ,

Que es la primera aproximación a la raíz de .
Evaluamos  .
Y hacemos nuestra tabla de signos,

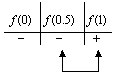
Puesto que  y    tienen signos opuestos, entonces la raíz se localiza en el intervalo  . 
En este punto, solo contamos con una aproximación, a saber,  , que es el primer punto medio calculado.
Repetimos el proceso, es decir, calculamos el punto medio ahora del intervalo  ,

Que es la nueva aproximación a la raíz de  .
Aquí  podemos calcular el primer error aproximado:

Puesto que no se cumple el objetivo, continuamos con el proceso.
Evaluamos  . 
Y hacemos la tabla de signos:

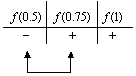
Puesto que   y    tienen signos opuestos, entonces la raíz se localiza en el intervalo  .
Calculamos el punto medio,

Y el nuevo error aproximado:

El proceso se debe continuar hasta que se logre el objetivo.
Resumimos los resultados que se obtienen en la siguiente tabla:         

Aprox. a la raíz	Error aprox.
0.5
0.75	33.33%
0.625	20%
0.5625	11.11%
0.53125	5.88%
0.515625	3.03%
0.5234375	1.49%
0.51953125	0.75%

De lo cual, vemos que la aproximación buscada es     
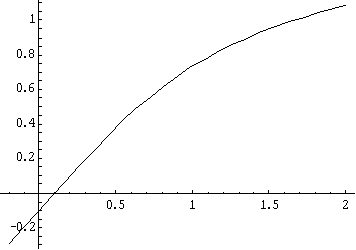
El método de bisección por lo general es lento, y en casos como el de la siguiente gráfica, puede ser demasiado lento.

En un caso como éste, el proceso de bisección comienza a acercarse a la raíz de forma muy lenta, ya que el método solamente toma en cuenta que la raíz se encuentra dentro del intervalo, sin importar si se encuentra más cerca de alguno de los extremos del intervalo. Sería bueno implementar un método que  tome en  cuenta este detalle.

Veremos a continuación un ejemplo del metódo de la bisección, con la siguiente ecuación:

Comenzar >>>