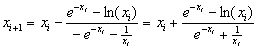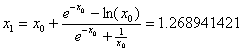Este método, el cual es un método iterativo, es uno de los más usados y efectivos. A diferencia de los métodos anteriores, el método de Newton-Raphson no trabaja sobre un intervalo sino que basa su fórmula en un proceso iterativo.
Supongamos que tenemos la aproximación    a la raíz    de  ,

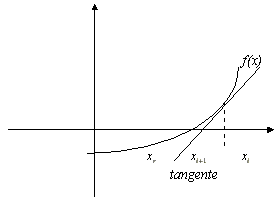
Trazamos la recta tangente a la curva en el punto  ; ésta cruza al eje    en un punto   que será nuestra siguiente aproximación a la raíz  .
Para calcular el punto  , calculamos primero la ecuación de la recta tangente. Sabemos que tiene pendiente

Y por lo tanto la ecuación de la recta tangente es:

Hacemos  :

Y despejamos  :

Que es la fómula iterativa de Newton-Raphson  para calcular la siguiente aproximación:

,   si

Note que el método de Newton-Raphson  no trabaja con intervalos donde nos asegure que encontraremos la raíz, y de hecho no tenemos ninguna garantía de que nos aproximaremos a dicha raíz. Desde luego, existen ejemplos donde este método no converge a la raíz, en cuyo caso se dice que el método diverge. Sin embargo, en los casos donde si converge a la raíz lo hace con una rapidez impresionante, por lo cual es uno de los métodos preferidos por excelencia.
También observe que en el caso de que  , el método no se puede aplicar. De hecho, vemos geométricamente que esto significa que la recta tangente es horizontal y por lo tanto no intersecta al eje   en ningún punto, a menos que coincida con éste, en cuyo caso   mismo es una raíz de  !
Ejemplo 1
Usar el método de Newton-Raphson, para aproximar la raíz de , comenzando con    y hasta que  .
Solución
En este caso, tenemos que

De aquí tenemos que:

Comenzamos con  y obtenemos:

En este caso, el error aproximado es,

Continuamos el proceso hasta reducir el error aproximado hasta donde se pidió.
Resumimos los resultados en la siguiente tabla:

Aprox. a la raíz	Error aprox.
1
1.268941421	21.19%
1.309108403	3.06%
1.309799389	0.052%

De lo cual concluímos que  , la cual es correcta en todos sus dígitos!
La misma idea puede aplicarse para crear algoritmos que aproximen raíces -ésimas de números reales positivos.
Observe que cuando el método de Newton-Raphson converge a la raíz, lo hace de una forma muy rápida y de hecho, observamos que el error aproximado disminuye a pasos agigantados en cada paso del proceso. Aunque no es nuestro objetivo establecer formalmente las cotas para los errores en cada uno de los métodos que hemos estudiado, cabe mencionar que si existen estas cotas que miden con  mayor precisión la rapidez ó lentitud del método en estudio.

Veremos a continuación un ejemplo del metódo de Newton Raphson, con la siguiente ecuación:

Comenzar >>>