Este método se basa en la fórmula de Newton-Raphson, pero evita el cálculo de la derivada usando la siguiente aproximación:

Sustituyendo en la fórmula de Newton-Raphson, obtenemos:

 

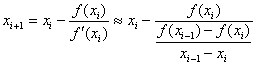
Que es la fórmula del método de la secante. Nótese que para poder calcular el valor de , necesitamos conocer  los dos valores anteriores    y  .

Obsérvese tambien, el gran parecido con la fórmula del método de la regla falsa. La diferencia entre una y otra es que mientras el método de la regla falsa trabaja sobre intervalos cerrados, el método de la secante es un proceso iterativo y por lo mismo,  encuentra la aproximación casi con la misma rapidez que el método de Newton-Raphson. Claro, corre el mismo riesgo de éste último de no converger a la raíz, mientras que el método de la regla falsa va a la segura. 

Ejemplo 1
Usar el método de la secante para aproximar la raíz de  , comenzando con  ,    y hasta que  . 

Solución
Tenemos que    y  , que sustituímos en la fórmula de la secante para calcular la aproximación  :

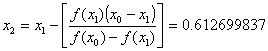
Con un error aproximado de:

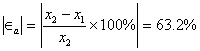
Como todavía no se logra el objetivo, continuamos con el proceso. Resumimos los resultados en la siguiente tabla:

De lo cual concluímos que la aproximación a la raíz es:

 

Ejemplo 2
Usar el método de la secante para aproximar la raíz de  , comenzando con    y  , y hasta que   . 

Solución
Tenemos los valores    y  , que sustituímos en la fórmula de la secante para obtener la aproximación  :

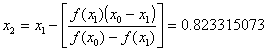
Con un error aproximado de:

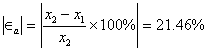
Como todavía no se logra el objetivo, continuamos con el proceso. Resumimos los resultados en la siguiente tabla:

  De lo cual concluímos que la aproximación a la raíz es:

Veremos a continuación un ejemplo del metódo de la secante, con la siguiente ecuación:

Comenzar >>>